RF-manBouncing Radio Off The Sky
I researched this topic a little, to satisfy my own curiosity. I then decided I'd put together this page
for the 'benefit' of other radio enthusiasts :o)
You are probably aware that radio hams playing on the 'HF' bands enjoy signals from all
over the world, where the radio waves have bounced off the sky. You may also know that powerful
rays from the Sun (ultra-violet, x-rays, gamma rays, etc ) break down atoms up there in
the sky, and this leads to loads of 'spare' electrons floating around. The number of
electrons in any given volume of sky (i.e. the density) varies with height, but NOT as a
straightforward drop the higher you go. The density changes rapidly at certain altitudes,
at layers you have probably heard of - the D layer, E layer, F layers etc. I am not going
to say too much more about this propagation mechanism when there's so much out there to read on
the Web.
A quick Web search will get you pages that include quick descriptions of the various
amateur HF bands -
searches like "propagation"+"e layer"+"critical angle" will be fruitful.
So, radio waves travel at slightly different speeds through different densities. A gradual
change of density doesn't do much to change the direction of a wave front hitting it from
an angle, but a larger rate of change in the density does. It is the change in density
that changes the direction of radio waves that makes DX possible. At VHF and UHF, it is
the change in water content in the air at different (relatively low) altitudes that makes
'tropo' happen - a high pressure system is forcing an air mass downwards and the rate
of density change increases. At HF though, it is whole loads of electrons whizzing about
up there that gives us a way of reflecting radio waves back down to Earth, because the
electron density changes rapidly at certain heights hundreds of km up.
There's a lot more to it, the more you read the more you realise there's more to know!
However, this page deals with one specific question...
I wondered if I could work out for myself just how far a signal will travel given a
definite elevation above the horizon and a definite height of the layer kindly providing
the bounce - leading to "What is the maximum range for a sporadic E hop from a point
barely above the horizon?".
The first thing to do is work out the distances involved. A few web searches revealed that
the metre was originally defined such that 10,000km was the distance from a pole to the
equater - a quarter of a Great Circle. This means that the radius of the Earth is the circumference 40,000km
divided by 2*pi which works out at 6366km. I use this figure despite numerous websites
reporting a variety of figures up to 6400, averaging at 6370! In fact the radius of the
Earth around the equator is usually reckoned to be 6,378 km, but the Earth is not a perfect
sphere. The "reference ellipsoid" and its dimensions have been precisely defined once and
for all by the IUGG in 1980: "The meridian is a perfect ellipse whose equatorial radius
is exactly a = 6,378,137m and whose polar radius is "approximately" b = 6,356,752.3141m."
Another search revealed the average effective height of the E-layer to be 105km above
average ground level, which is 6471km from the center of the planet.
First of all, I drew a quick diagram. A circle to represent the Earth, another for the E layer,
and a horizontal line from a transmitting station on the top of the planet. How to work out exactly
where this line reaches the outer circle - and so work out how far the maximum hop would be.
Hmmm, circles. This looks a bit tricky, I thought!
After a bit of puzzling, it dawned on me it could actually be extremely simple. It was probably
just a bit of sine or cosine tomfoolery. A few more diagrams and I had it solved. This gave a
glow of smug satisfaction that lasted long enough for me to write this page.
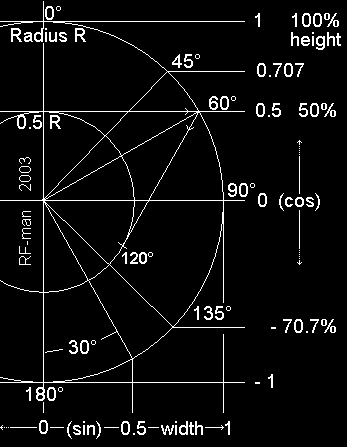
Cosines. Handy things when working with circles. The sine and cosine curves are simply
derived from the height above the center of the circle of a point on the edge of the circle
at particular angles. You what? Have a look at this then :
Ignore the inner circle to start with. The outer circle with a radius of 1 unit is the important
one. As we sweep around the circle from 3 o'clock (90 degrees) through 360 degrees back to 3 o'clock again,
plot the height on a graph from 0.0 up to 1.0, down again etc - you'll see a sine wave.
So that's how it works! The cosine simply
starts at 12 o'clock (1.0) instead, 90 degrees out of phase.
Dial 60 into a scientific calculator and press the [cos] button. It'll give the result 0.5 - if it doesn't
you've either pressed the wrong button or your calculator is using a different way of specifying angles.
There are 360 degrees around a circle, 400 gradians (or grads), or approx 6.28 radians (2 x Pi). Don't worry about
these until you ever have to deal with them. I've only twice needed to - most programming languages seem
to only work in radians and need some tweaking to deal with degrees.
It should be obvious from the diagram above that if the E layer had twice the radius of the Earth, then
a signal beamed at the 'horizon' from the top of the inner circle will hit the outer circle at the point
labelled 60 degrees. Therefore a reflection will graze the inner circle at 120 degree from the top.
This is just what we need to solve our problem. When the inner circle is 0.5 times the radius of the
outer circle, the angle around the circle is the [inverse] [cos] of 0.5 ... 60 degrees.
If you can face trying another, try drawing the two circles with the inner being 70% of the outer,
and you'll probably get the familiar 45 degrees.
Now we'll change the numbers to represent the real radius of the Earth and the Earth + E layer.
The inner circle is 6366km, and the outer circle is 6366+105=6471km. Quite close circles!
The Earth circle is 0.983773 (etc) of the width of
the E-layer circle, or 98.377 per cent of it.
Now instead of using the 0.5 or 0.707 in
the paragraph above, use 0.983773 instead. By using the inverse cos button on the calculator
we find that the angle is 10.3356 (approx) degrees.
So, we have found out that by the time someone has travelled 10.3356 degrees around the
real world away from you, the E-layer directly above their head is right on your horizon.
If you could bounce a radio signal off that point, you could reach 20.6712 degrees around
the globe. 20.6712 ninetieths of 10,000km means that the range would be some 2296km!
(That 10.3356 degree point being 1148km away) A little further simple maths reveals that the
sine of 10.3356 multiplied by 6471 gives the distance the radio wave travels to that point - 1161km.
This seems to tie in nicely to the following quote I found -
"In the classical model, sporadic-E reflections are assumed to be specular (mirror-like)
and associated with a single E cloud that lies midway along a given radio path at an
altitude of about 105km. At this altitude the maximum possible single-reflection
(single hop) distance computes to about 2200 km." And for those of us who still think in
terms of miles, divide by 1.609344 (too precise perhaps!) and that 2200km is 1367 miles.
For F2 at 450km, 20.936 * 2 = 41.87 degrees, 4652km. For 600km, 23.95 * 2 = 47.9, 5323km. So 4 or 5 times the
altitude of the E layer and the range is only in the order of twice of that from the E layer.
So here's a scale diagram that should help you get a real idea of what's going on - not like
the usual diagrams we get of these things where a single hop would reach from pole to pole!
While I was at it, I did more maths for an F2 hop from 500km up, and I added a few bits to
show the size of other planets and the moon. How very educational.
Scroll to the upper right quadrant to see the important bit, if you need to. Then get a bigger monitor! ;o)
|
The whole GIF picture is only 24k. Splendid.

So the main calculation that sparked off all of this has been sorted.
Hoorah. Now comes the tricky part, how far do you get for any given elevation above
0 degrees from the horizon? Or, if you can only get a signal as low as 5 degrees, what range
can you expect? If we halve the angle around the world, we halve the range too. But what elevation
does this correspond to? A little bit of sin and cos magic gives us the coordinates of the reflecting
point for any angle. (Cos 5.1678) * 6471 gives a point 6444.7km up from the center of the Earth, which is 78.7km
above the transmitting station, and (Sin 5.1678) * 6471 tells us it's 582.86km along the flat 1161km line.
A little cheating is in order here, using Rectangular to Polar coordinates conversion on my trusty Casio
calculator. 582.9 [R to P] 78.7 [=] shows a 588 km distance, and a press of the [X to Y] button reveals
the angle upwards of 7.8 degrees. Beats working it out by hand, doesn't it?!
proportion of max deg km along km up angle of elev range (km) 100% whole 10.3356 1161 0 0 2296 50% half 5.1678 582.9 78.7 7.8 1148 25% qtr 2.5839 291.72 98.42 18.6 574 12.5% 8th 1.29195 145.9 103.35 35.3 287 * 8.9% 0.92231 104.16 104.16 45 205 * 6.25% 16th 0.645975 72.955 104.58 55.1 143 * * angle of incidence too great for sporadic E reflection Out of interest, freespace path loss in dB = 32.45 + 20 log10 MHz + 20 log10 km, or 133dB over a 2200km path on 6m. A distant 100W ERP station (+50dBm) could lose 143dB in transit and still reach us at -93dBm which is enough for an S9 on the meter. So, I believe this shows that somebody living in a valley (or on a hillside shielded from the best directions) has virtually no chance if they cannot see the sky at elevations of less than some 20 degrees or so.
Well that was fun. Just don't ask what difference a nice height Above Sea Level would make :o)
So now we can plug in some real numbers, dividing the radius of the Earth by the same figure plus the extra height, and then inverse cosines will tell us how far around the world we've shifted the equivilant sea-level transmitting point. For example an elevation 100m above terrain that is flat to the horizon will give you about 35km more range - as if you were transmitting from a point 0.32 degrees further around the planet (35km from where you are). Even from a million miles above your QTH, a signal will meet a horizon almost but not quite 90 degrees around from you. Example 0.1km ASL : (6366/6366.1) inv cos = 0.3211 degrees ... 0.3211 / 360 x 40000 km = 35.68 km Example 1km ASL : (6366/6367) inv cos = 1.0155 degrees ... 1.0155 / 360 x 40000 km = 112.83 km Example 10km ASL : (6366/6376) inv cos = 3.2094 degrees ... 3.2094 / 360 x 40000 km = 356.6 km Example 105km ASL : (6366/6471) inv cos = 10.3356 degrees ... 10.3356 / 360 x 40000 km = 1148.4 km Example 1000km ASL : (6366/7366) inv cos = 30.2038 degrees ... 30.2038 / 360 x 40000 km = 3356 km Example 2636.8 ASL : (6366/9002.8) inv cos = 45 degrees ... 45 / 360 x 40000 km = 5000 km Example million! : (6366/1006366) inv cos = 89.6375 degrees ... 89.6375 / 360 x 40000 km = 9959.73 km In a nutshell, with practical ASLs any extra height really won't affect range much if you can already see the horizon, and moving to a higher location is likely to be much of a waste of time. With multiple hop paths you're still only affecting the first hop, by a small fraction. If you'd like a Great Circle Map centred upon London, with rings at 2300km, 5000km, 10000km labelled E, F2, 2 x F2 click here (new window).
While I'm compiling a page like this, I might as well add a few other notes I found, while trying to decode all the ionospheric mumbo jumbo at the end of the GB2RS news bulletin.
Solar activitySolar Flux is a measurement of the intensity of solar radio emissions, proportional to sunspot activity. The level of the sun's ultraviolet and X-ray emissions is primarily responsible for causing ionization in the earth's upper atmosphere. Solar activity can be summarised by daily measurements of solar radiation at a wavelength of 10.7cm (F10.7), 2.8GHz, given in solar flux units (sfu). 1 sfu = 10-22Watts/meter2 Hz = 104 jansky. (Karl Jansky 1905-1950) sfu readings range from a theoretical minimum of approximately 67 to actually-observed numbers greater than 300.
Solar X-ray flux readings are measured at nanometre wavelengths rather than the 10.7cm (2.8GHz) used
for sfu. Solar x-rays occupy a wide range of wavelengths with the portion used for Solar Flare
classification from
0.1 through 0.8 nm (X-rays span 3 orders of magnitude, 10 to 1, 1 to 0.1, and 0.1 to 0.01 nanometres).
The following classifications are used for measurement :
Solar X-ray activity levels
Large solar x-ray outbursts can produce sudden and extensive ionization in the lower regions of the earth's ionosphere which can rapidly increase shortwave signal absorption there. Occurring on the sun-facing side of the Earth, these SID Sudden Ionospheric Disturbances are known as 'shortwave fadeouts' and can degrade short wave communications for from minutes to hours.
Geomagnetic ActivityGeomagnetic activity includes anything that upsets the magnetic field that surrounds the earth. Things that can disrupt this field include solar dust (which comes off of the sun during a solar flare) and other charged space dust. The A index can range from 0 up to 40 or even higher. A lower number indicates that the geomagnetic field is less disturbed. The higher the A index climbs, the "louder" the noise on the bands becomes. Quite bands, therefore, correspond to low A indexes. Quiet bands allow weaker signals to come through more clearly, as there is less noise to interfere. The K-Index is useful in determining the state of the geomagnetic field, the quality of radio signal propagation and the condition of the ionosphere. Generally, K index values of 0 and 1 represent Quiet magnetic conditions and imply good radio signal propagation conditions. Values between 2 and 4 represent Unsettled to Active magnetic conditions and generally correspond to less-impressive radio propagation conditions. K-index values of 5 represent Minor Storm conditions and are usually associated with Fair to Poor propagation on many HF paths. K-index values of 6 generally represent Major Storm conditions and are almost always associated with Poor radio propagation conditions. K-index values of 7 represent Severe Storm conditions and are often accompanied by "radio blackout" conditions (particularly over higher latitudes). K-indices of 8 or 9 represent Very Severe Storm conditions and are rarely encountered (except during exceptional periods of solar activity, one example being a large X45 flare in Oct 2003). K-indices this high most often produce radio blackouts for periods lasting in excess of 6 to 10 hours (depending upon the intensity of the event). The K index is the result of a 3-hourly magnetometer measurement comparing the current geomagnetic field orientation and intensity to what it would have been under geomagnetically 'quiet' conditions. K index measurements are made at sites throughout the globe and each is carefully adjusted for the geomagnetic characteristics of its locality. The scale used is quasi-logarithmic, increasing as the geomagnetic field becomes more disturbed. K indices, first introduced by J. Bartels in 1938, consist of a single-digit 0 thru 9 for each 3-hour interval of the universal time day (UT). Kp 9 = Ap 400. The official planetary Kp index is derived by calculating a weighted average of K-indices from a network of geomagnetic observatories (Kp = "planetarische Kennziffer" = planetary index). The conversion table for the Boulder magnetometer is shown below:
The A-index was invented because there was a need to derive some kind of daily average level for geomagnetic activity. Because of the non-linear relationship of the K-scale to magnetometer fluctuations, it is not meaningful to take averages of a set of K indices. What is done instead is to convert each K back into a linear scale called the "equivalent three hourly range" a-index (note the lower case). The daily A index is merely the average of eight "a" indices. The following table illustrates the conversion between K and "a":
(NOAA Geomagnetic Storm levels are from G1 to G5 at Kp indexes of 5 to 9) The daily index Ap is obtained by averaging the eight values of ap for each day - 8 "a" indexes are added together and divided by 8 to give "A". The p (as in "Ap" and "ap") simply means "planetry". http://www.estec.esa.nl/wmwww/wma/Data_Plots/noaa/ap_plot.html
Bz = southward IMF (interplanetory magnetic field), nanoTeslas. The Dst (Disturbance Storm Time) is a geomagnetic index which monitors the world wide magnetic storm level. It is constructed by averaging the horizontal component of the geomagnetic field from mid-latitude and equatorial magnetograms from all over the world. Negative Dst values indicate a magnetic storm is in progress, the more negative Dst is the more intense the magnetic storm. The negative deflections in the Dst index are caused by the storm time ring current which flows around the Earth from east to west in the equatorial plane. The ring current results from the differential gradient and curvature drifts of electrons and protons in the near Earth region and its strength is coupled to the solar wind conditions. Only when there is an eastward electric field in the solar wind which corresponds to a southward interplanetary magnetic field (IMF) is there any significant ring current injection resulting in a negative change to the Dst index. Thus, by knowing the solar wind conditions and the form of the coupling function between solar wind and ring current, an estimate of the Dst index can be made.
17 Mar 2004 Click > Return to the home page menu < Click |